Геометрия на iPad: лучшие из лучших
Когда-то на этом самом сайте я затеял было писать статьи о геометрических приложениях для iPad. И даже написал две… после чего понял, что пытаюсь обнять необнимаемое и впихнуть его в невпихуемое. (: Нет, серьёзно — тема, при всей моей любви к ней, оказалась неподъёмной и непродвигаемой.
К сожалению, главная причина в языке. Менталитет Этой Страны не одобряет знание иностранных языков, и этим очень многое сказано. Ну расскажу я о замечательной интерактивной версии „Начал“ Эвклида с произвольно перестраиваемыми чертежами — и что толку? На английском же. И таких приложений немало.
Посему тему я закругляю, благо о самом интересном уже успел рассказать здесь и здесь. Но при этом считаю своим моральным долгом поведать о двух абсолютно лучших приложениях, мимо которых любителям геометрии уж точно проходить нельзя. Об одном, правда, рассказ уже был, но оно с тех пор успело радикально поменяться в лучшую сторону. Другое уникально по своей мощи и к тому же бесплатно. Итак, поехали.
Прежде чем их обозревать, нужно пояснить важнейшую концепцию в мире геометрических компьютерных приложений, имя которой — динамическая геометрия. Попробую сделать это так:
Системы динамической геометрии представляют чертёж не только координатами содержащихся на нём объектов, но и логическими взаимосвязями между ними.
Для знакомых с программированием можно сказать и так, что динамическая геометрия представляет собой „объектно-ориентированный“ чертёж: на нём свойства и характеристики построенных объектов наследуются. То есть, к примеру, вы построили прямую а как серединный перпендикуляр к отрезку АВ, и точки её пересечения с окружностью b обозначили C, D. Если теперь изменить положение одной из исходных точек (А или В), то и прямая, и точки её пересечения с окружностью, и всё что далее было построено в зависимости от них, — всё это автоматически перестроится, так что чертёж будет отображать новую ситуацию. Это позволяет наглядно исследовать разные варианты, показывать сложные зависимости и закономерности, и делать ещё много чего. Первое из наших двух приложений именно таково. Встречаем —
GeoGebra
Сначала немного предыстории. Это очень известное мультиплатформенное приложение с очень богатыми возможностями. И оно по жизни было бесплатным… да, собственно, и сейчас является таковым. Так вот, в прошлом 2013 году разработчики задумали выпустить его ещё и для планшетов. По поводу чего затеяли сбор средств через KickStarter. Объявив при этом, что если требуемая сумма наберётся, то планшетный результат тоже будет халявным.
То есть, фактически, попросили денежку просто так. Подайте нам на выпуск планшетной версии, а вам за это ничего не будет, кроме „спасибо“. И ведь набрали требуемую сумму, как говорится, со свистом. Что весьма недвусмысленно говорит о популярности их разработки.
Приложение представляет собой ярко выраженную динамическую геометрию с большим набором „макросов“ — типовых построений циркулем и линейкой, из которых, как из кирпичиков, складывается решение более сложных задач на построения. Помимо чистой геометрии, можно работать с функциями, их графиками, кое-какими алгебраическими преобразованиями и кое-чем ещё, но здесь GeoGebra всё же уступает специализированным программам типа QuickGraph или WolframAlpha. И не всё из этого продвинутого функционала было реализовано для планшетов.
Посмотрим на окно приложения. Выглядит оно вот так:
В верхнем левом углу настраивается внешний вид объектов: какого цвета они должны быть, какую линовку иметь и т.п. С правой стороны экрана — выдвижная панель со списком объектов, где можно управлять их определениями и видимостью. Ну, а внизу — основные инструменты программы. Опишу их подробнее.
Идём слева направо. За первой кнопкой кроются средства перемещения, стирания и поворота объектов. Вторая кнопка — расстановка точек (здесь же нахождение средней точки между двумя заданными). Третья кнопка — отрезки, лучи, прямые и векторы. Четвёртая — параллели, перпендикуляры, биссектрисы и касательные. Пятая — многоугольники. Шестая — окружности, полуокружности, дуги и секторы. Седьмая — конические сечения: параболы, эллипсы, гиперболы и коники общего вида по пяти точкам. Восьмая — задание и измерение расстояний и углов. Девятая — преобразования симметрии, инверсии и гомотетии. Десятая — ручное рисование произвольных кривых. Ну и, наконец, последняя одиннадцатая — задание параметрических ползунков, позволяющих оперативно влиять на объекты чертежа.
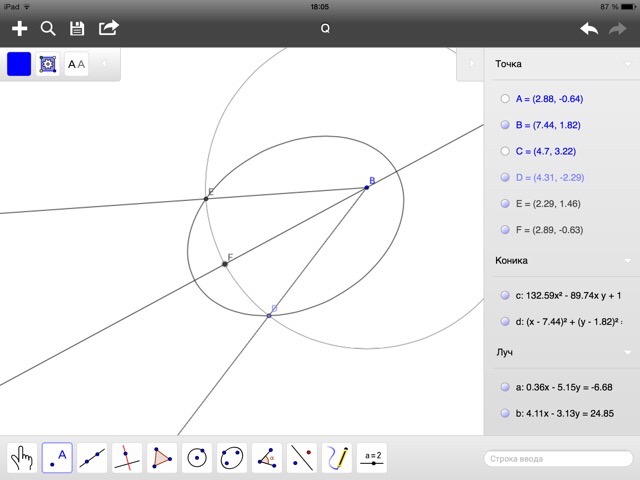
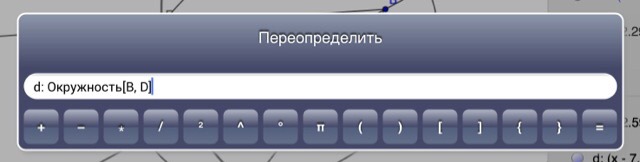
Справа внизу находится строка ввода, которая позволяет при желании задавать геометрические объекты не рисованием по экрану, а аналитическим описанием. Приложение имеет свой собственный язык, который выглядит вполне естественно, причём локализован, так что можно писать по-русски:
То есть, если вам нужно построить окружность с центром B и радиусом ВD, вы можете выбрать соответствующий инструмент и последовательно ткнуть две точки чертежа — а можете написать в строке ввода то, что видите выше. При наличии внешней клавиатуры второй способ много удобнее. Выбор языка ввода — на ваше усмотрение (мне проще по-английски).
В качестве иллюстрации — вот так выглядит в GeoGebra решение классической задачи на построение: по данному прямоугольнику построить равновеликий квадрат.
Планшетная версия этого замечательного приложения в целом сохраняет геометрические возможности десктопной, но имеет две особенности, которые нужно иметь в виду.
Во-первых и главных, планшет таки сильно уступает настольному компьютеру по вычислительной мощности. В обычных условиях эвклидовой геометрии это незаметно, но… Если вы попытаетесь работать с кривыми более высокого, чем второй, порядка — заурядной лемнискатой, например, — то запросто можете поиметь неслабые тормоза. То же самое получится, если вы увлечётесь украшательствами и начнёте проводить на чертеже всякие пунктирные и штрихпунктирные линии — очень не рекомендую делать это! Ограничьтесь цветной раскраской.
Во-вторых, разработчики очень странно подошли к вопросу хранения и импорта-экспорта чертежей. Всё что вы начертите, будет храниться внутри приложения, и это естественно. Вы можете закидывать чертежи на специализированный сервис разработчиков (он называется GeoGebraTube) и загружать чертежи оттуда. И… и это, собственно, всё.
Средств экспорта чертежа в векторную или растровую графику нету. Средств обмена чертежами с настольным компьютером посредством iTunes тоже нету! По крайней мере, штатных. Можно лишь работать методом „открыть в…“ через „облака“ (Dropbox, Evernote…) при условии, что у вас на планшете и десктопе стоят соответствующие приложения. Это не то чтоб сильно неудобно, но требует определённой привычки. В конце концов, на планшете обычно лишь набрасывается общая идея, а до ума она доводится на десктопе — где мышь позволяет позиционировать точки намного аккуратней, — и где есть мощные средства экспорта в любой желаемый формат.
Но по богатству возможностей с GeoGebra на iPad не сравнится ничто, и за это ей можно простить всё что угодно. К тому же бесплатно — абсолютно бесплатно, ни рекламы, ни встроенных покупок, ничего. Брать здесь. А главный сайт приложения, откуда можно скачать десктопные версии, здесь.
Isosceles
В отличие от предыдущего случая, это приложение представляет собой не динамическую геометрию, а эмулятор циркуля и линейки. Из „динамики“ здесь доступно всего четыре элемента: биссектриса угла, деление отрезка пополам, серединный перпендикуляр к отрезку и правильный многоугольник.
Могут спросить: а зачем про это рассказывать, если динамическая геометрия заведомо более мощна и функциональна? Вопрос логичный, и на него есть ответ.
Дело в том, что геометрический чертёж далеко не всегда нужен в качестве средства демонстрации или исследования. Иногда он нужен просто как иллюстрация — в статью, книгу или на веб-страницу, — и вот тут „ручные“ средства построений зачастую имеют преимущество. Просто потому, что позволяют начертить ровно то, что требуется, не больше и не меньше. А вот объяснить это автоматике далеко не всегда легко и просто. (:
В прошлом 2013 году мне довелось провести для старшеклассников небольшой курс о геометрических построениях и их связи с алгебраическими проблемами — как основной инструмент мы использовали сочетание iPad + Isosceles. А когда я постфактум изложил этот курс в виде книжки, то все иллюстрации делал тоже в Isosceles. Просто потому, что ничего удобнее не знаю. Экспортировал в PDF (это можно делать прямо с планшета), так в итоге и издали…
Посмотрим на интерфейс.
В левом нижнем углу — кнопка вызова „файлового менеджера“, в правом нижнем — текстовой панели для заметок и пояснений. Справа вверху кнопки экспорта, настроек (там же справка) и undo/redo. Внизу в центре основные инструменты.
Первая кнопка — переключение режима карандаша. Это фирменная фишка приложения: чертить можно как „главным“ карандашом, так и вспомогательным. В первом случае все объекты будут чёрного цвета и точкам будут автоматически присваиваться имена, во втором случае используется серый цвет и точки не именуются. Очень удобно, позволяет не засорять чертёж лишними деталями.
Вторая кнопка — задание точек на чертеже. Третья кнопка — проведение отрезков между точками. (Если нужна прямая, то в свойствах отрезка его нужно „расширить“, а лучи в приложении не предусмотрены.) Четвёртая кнопка — окружности. Пятая — циркуль (это вторая „фишка“ приложения, о которой позднее). Шестая — правильные многоугольники. Следующие три — конические сечения (парабола, эллипс, гипербола). Далее идут две кнопки для нанесения на чертёж текста и формул, а также инструмент произвольного рисования.
В качестве иллюстрации того, как этими инструментами можно пользоваться, вот видео простенького построения — прямой угол, имеющий вершину в данной точке.
А теперь немного комментариев. В программе совершенно замечательно реализован циркуль — и обратите внимание, что он вынесен отдельно от проведения окружностей. Окружность строится полностью по центру и радиусу, тогда как циркуль позволяет проводить произвольные дуги с измерением расстояний по чертежу.
Сделано точно как в натуре. Вы видите положения двух ножек циркуля и соответствующую им будущую окружность. Перемещая ножки, делаете измерение по чертежу — раствор циркуля устанавливается в будущий радиус. Затем перетаскиваете одну ножку в будущий центр и проводите нужную дугу. Просто и естественно.
Конические сечения задаются немного непривычно — вместо обычных способов „фокус-фокус“ и „фокус-директриса“ здесь используются сочетания „центр-фокус“ и „вершина-фокус“. Задержав палец на соответствующей кнопке, можно задать конику её уравнением, но это сделано не очень удобно и с рядом ограничений.
Наконец, нужно упомянуть инструмент нанесения формул на чертёж. Если его активировать, то вы увидите обычный текстовый ввод (с добавленной панелькой математических символов) — но после завершения программа попытается интерпретировать введённое как выражение и отформатировать его. Получается примерно так:
Не очень красиво, но для простейших случаев сгодится.
Многие вещи можно делать через контекстное меню чертежа. В предложенном видеоролике таким образом показывается величина угла и „продлевается в прямую“ отрезок. Оттуда же задаются цвета и оформление точек-линий.
В целом интерфейс Isosceles нельзя назвать интуитивным, но… привыкнув к нему единожды, очень быстро начинаешь считать его естественным. (: Но справка только на английском, так что в случае чего привыкать придётся методом тыка.
Все чертежи сохраняются в iCloud, причём занимают очень мало места. Но тут нужно иметь в виду одну особенность: на миниатюрах в файловом менеджере видны только те линии, которые нарисованы „основным“ карандашом, поэтому выглядит немного непривычно. (: Лучше давайте своим чертежам „говорящие“ названия.
Ну и самое главное. Приложение платное. Полная версия стоит 169 рублей. Существует и бесплатный вариант, имеющий следующие ограничения:
- Работает одновременно не более чем с двумя документами.
- Недоступна часть инструментов: ввод формул (невелика потеря) и конические сечения (вот это уже серьёзней).
- Недоступны некоторые продвинутые возможности вроде полярных координат и изометрических сеток.
- Сильно ограничены возможности экспорта (только сохранение картинки в „фотоплёнку“).
- Недоступно большинство уроков и тестов (которые всё равно на английском).
Если вы скачаете бесплатный вариант, то разблокировать недоступные инструменты встроенной покупкой будет стоить 99 рублей, и ещё по 33 рубля нужно выложить за каждый из трёх или четырёх уроков. Результат будет отличаться от полной версии только цветом иконки и подписью под ней. (: Если вы попробуете бесплатную версию (пусть и разблокированную), а потом раскошелитесь на отдельную платную, то все чертежи у вас сохранятся.
А вам слабо?
Для тех, кто действительно интересуется геометрией, вот небольшая подборка моих любимых задач на построение, которые я традиционно подсовываю школьникам и студентам. (: Если не сказано иного, то построение требуется выполнить классическим „эвклидовым набором“ инструментов: циркуль произвольного раствора и односторонняя линейка без отметок.
- По данному ромбу построить вписанную в него окружность.
- По данной окружности и точке вне её построить ромб, для которого эта точка совпадёт с вершиной одного угла, а окружность окажется вписанной.
- Дана окружность с неизвестным центром и лежащая на ней точка А. Пользуясь одним только циркулем, построить такую точку В, что прямая АВ является касательной к окружности.
- По числу 0<х<1, заданному длиной отрезка, построить такие углы, синус и косинус которых равен этому числу.
- Построить углы величиной (в градусах) 48, 27, 9, 6.
- Односторонней линейкой без отметок и циркулем неизменного раствора разделить пополам отрезок, длина которого превышает раствор циркуля более чем вдвое.
- Построить окружность, касающуюся двух данных прямых и проходящую через данную точку на одной из них.
- Построить квадрат, три вершины которого лежат на трёх данных (различных) параллельных прямых.
- Для данного эллипса с известными фокусами построить касательную через лежащую на нём точку.
- По данной параболе с известным фокусом построить её директрису.
- По данной параболе с известной директрисой построить её фокус.
- По данной параболе с известными фокусом и директрисой построить касательную через лежащую на ней точку.
- По данной гиперболе с одним известным фокусом построить её второй фокус.
- По данной кардиоиде построить её внутреннюю неподвижную окружность.
- По данной лемнискате Бернулли построить её большую ось симметрии и фокусы.
Две последние задачи нужно решать в GeoGebra: кардиоида и лемниската представляют собой кривые более сложной природы, чем конические сечения, и Isosceles не имеет средств для работы с ними.








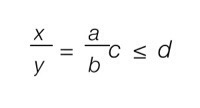

“К сожалению, главная причина в языке. Менталитет Этой Страны не одобряет знание иностранных языков, и этим очень многое сказано.”
Вы же позволяете себе употреблять такие слова как гипербола, кардиоида или лемниската :D И вам как человеку с аналитическим складом ума не странно и не оскорбительно – прежде всего для себя – швыряться кванторами всеобщности? Так что можно было хотя бы упомянуть нелокализованные программы – появится интерес и язык выучат (хотя бы несколько слов для понимания интерфейса, это ведь совсем просто)
По-моему, процитированной фразой я утверждаю не всеобщность, а яркую тенденцию. И в этом утверждении убеждён абсолютно — многие поколения школьников и студентов убедили. Ничего оскорбительного здесь не вижу ни для них, ни для себя, ибо объективная реальность. Мог бы рассказать в эту тему несколько историй, но здесь это оффтопик.
Что касается рассказов о нелокализованных программах — ну перечитайте мои материалы на этом сайте. (: Когда дело того действительно стоит, мне совершенно не лень подготовить какую-никакую собственную документацию, но на это нужно вдохновение. (:
А вот насчёт «появится интерес и язык выучат» — извините, мне на это утверждение просто смешно. Абсолютное большинство ничего учить не подумает, а тупо отпишется в духе «напешите чиво нажимать атофсё нипаруски и я ничо непонел». Пройдено многократно.
“Менталитет Этой Страны”
Ищите другую. Мой Вам совет.
Да, да! Именно так нужно ответить человеку с техническим образованием и знанием языка, которого ждут с распростертыми руками в любой стране мира, а он, вместо этого, пытается вложить что-то в головы студентов, чтобы как-то поднять свою страну. Даже и “Страна” написал с большой буквы, между прочим. Спасибо нужно сказать, что еще не нашел другую.
Простите за оффтоп, обидно.
З.ы. На счет менталитета – согласен на все 100.
“Спасибо нужно сказать, что еще не нашел другую.”
Видимо эта Страна хорошо кормит.
Дискуссия прекращена. Сайт не об этом. Извиняюсь, если кого обидел.
Хоть я и достаточно далек от математики с геометрией, но статьи Михаила всегда читаю с удовольствием.
Соглашусь, для многих (в том числе и для меня) язык имеет ключевую роль. Обидно, когда, скажем, есть локализация для суоми, а великий могучий обошли стороной.
Очень здорово! Побольше обзоров от этого автора!
В промежутке между написанием и опубликованием этой статьи успела выйти версия 3.0 приложения Isosceles. Немного поменялся интерфейс, но возможности принципиально не изменились. Кроме того, проскочила информация от разработчиков Geogebra, что они готовят апдейт приложения к новому учебному году (читай — к сентябрю).
Картина маслом: 2 часа ночи я нашла циркуль и сижу рисую кружочки высунув язык от усердия и старательности ))) Все получилось, много заданий сделала :) не зря в школе училась :) спасибо за обзор, скорее всего не понадобятся мне эти приложения, но все равно интересно :)
Автор пишет “К сожалению, главная причина в языке. Менталитет Этой Страны не одобряет знание иностранных языков, и этим очень многое сказано. Ну расскажу я о замечательной интерактивной версии „Начал“ Эвклида с произвольно перестраиваемыми чертежами — и что толку? На английском же. И таких приложений немало.”
Вот и нужно рассказывать. И менталитет поменяется. В конечном итоге, основная причина изучения иностранного языка – это стимул. Дальше можно сказать много пафосных слов об этом самом стимуле, технологиях и прочем, но смысл будет простым: сначала появляется желание узнать. А разве не об этом все ваши статьи? :)